Zuerst einmal können wir uns überlegen, was beim Laden bzw.
Entladen eines Kondensators passiert. Zu Beginn des Ladevorgangs befinden sich
keine Ladungen auf dem Kondensator, er ist leer. D.h. zum Zeitpunkt ![]() ist die Ladung
ist die Ladung ![]() und damit ist auch die Spannung am Kondensator
und damit ist auch die Spannung am Kondensator ![]() . Nun fließt zum Laden ein Strom auf den Kondensator. Da zu
Beginn keine Ladungen darauf sind, ist dieser Strom maximal. Der Strom bringt
nun Ladungen auf den Kondensator, so dass
. Nun fließt zum Laden ein Strom auf den Kondensator. Da zu
Beginn keine Ladungen darauf sind, ist dieser Strom maximal. Der Strom bringt
nun Ladungen auf den Kondensator, so dass ![]() größer wird und auch die Spannung am
Kondensator steigt nun. Je mehr Ladungen auf dem Kondensator sind, desto größer
ist das Potential am Kondensator und desto kleiner ist der Potentialunterschied
zwischen Spannungsquelle und Kondensator. Da der Potentialunterschied aber der
Antrieb für den Stromkreis ist, sinkt die Stromstärke I. Ist der Kondensator
vollgeladen, so bleiben
größer wird und auch die Spannung am
Kondensator steigt nun. Je mehr Ladungen auf dem Kondensator sind, desto größer
ist das Potential am Kondensator und desto kleiner ist der Potentialunterschied
zwischen Spannungsquelle und Kondensator. Da der Potentialunterschied aber der
Antrieb für den Stromkreis ist, sinkt die Stromstärke I. Ist der Kondensator
vollgeladen, so bleiben ![]() und
und ![]() konstant und
konstant und ![]() ist
ist ![]() , es fließt kein Strom mehr.
, es fließt kein Strom mehr.
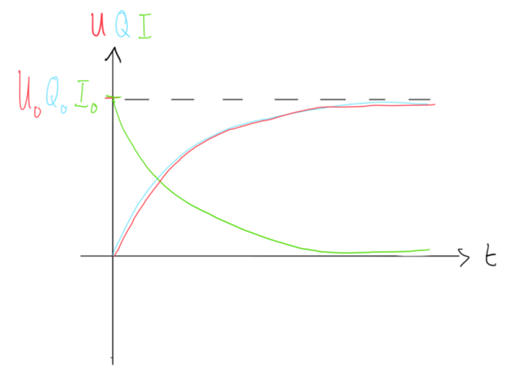
Beim Entladen befindet sich nun die maximale Anzahl von
Ladungen auf dem Kondensator. D.h. die Spannung am Kondensator und die Ladungen
darauf sind zum Zeitpunkt ![]() maximal. Lässt man nun zu, dass sich der Kondensator
entlädt, z.B. durch Anschließen eines Verbrauchers, dann fließt ein Strom. Da
viele Ladungen vorhanden sind, der Potentialunterschied zum Verbraucher hoch
ist, ist die Stromstärke groß. Dadurch sinken die Anzahl der Ladungen und die
Spannung am Kondensator stark. Je weniger Ladungen sich auf dem Kondensator
befinden, desto kleiner wird die Stromstärke, da natürlich der Potentialunterschied
kleiner wird. Also sinken auch
maximal. Lässt man nun zu, dass sich der Kondensator
entlädt, z.B. durch Anschließen eines Verbrauchers, dann fließt ein Strom. Da
viele Ladungen vorhanden sind, der Potentialunterschied zum Verbraucher hoch
ist, ist die Stromstärke groß. Dadurch sinken die Anzahl der Ladungen und die
Spannung am Kondensator stark. Je weniger Ladungen sich auf dem Kondensator
befinden, desto kleiner wird die Stromstärke, da natürlich der Potentialunterschied
kleiner wird. Also sinken auch ![]() und
und ![]() . Alle drei Größen sinken, bis sie 0 erreichen.
. Alle drei Größen sinken, bis sie 0 erreichen.
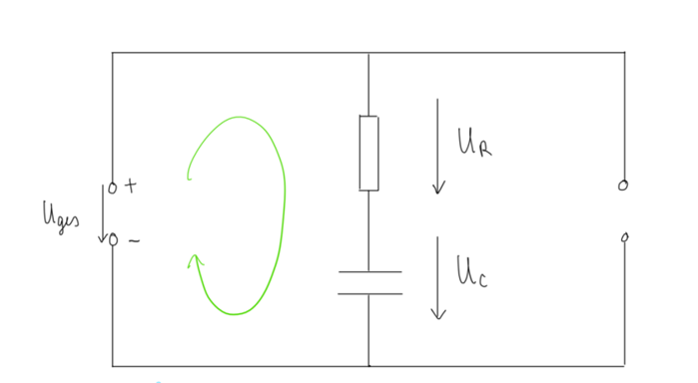
1. Entladen:
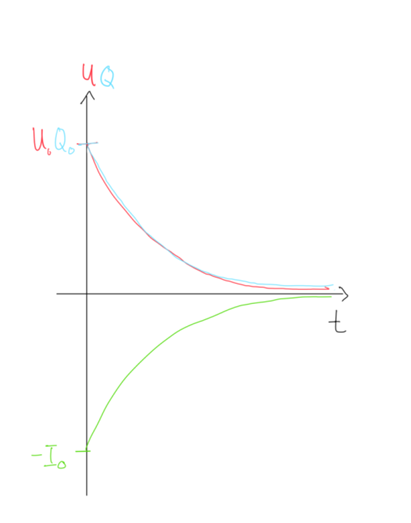
Bei der Grundschaltung handelt es sich um eine Reihenschaltung, d.h. der Strom ist konstant und die Spannungen werden addiert (Maschenregel):
![]()
![]()
Beim Entladen ist die angelegte Spannung ![]() :
:

Im letzten Schritt verwendet man den Zusammenhang ![]() . Also können wir den Strom als Ladungsänderung (zeitliche
Ableitung von
. Also können wir den Strom als Ladungsänderung (zeitliche
Ableitung von ![]() entspricht
entspricht ![]() ) schreiben. Als nächstes können wir die Gleichung so
umstellen, dass
) schreiben. Als nächstes können wir die Gleichung so
umstellen, dass ![]() alleine steht:
alleine steht:
![]()
Dies nennt man homogene Differentialgleichung (DGL). Im
Folgenden könnt ihr sehen, wie man diese einfache Art der DGL lösen könnt.
Homogene DGLs der 1.Ordnung haben immer die Form ![]() . Wichtig ist dabei, dass wir
. Wichtig ist dabei, dass wir ![]() als Angabe der Ableitung aus Mathe kennen.
als Angabe der Ableitung aus Mathe kennen.
![]() und
und ![]() kommen auch in der Integralrechnung
vor. Um diese Art der DGL lösen zu können, solltet ihr deshalb mit der
Integralrechnung vertraut sein. Die Integralrechnung ist die Umkehrrechnung der
Differenzialrechnung. Mit diesem Wissen können wir die Gleichung lösen. Schaut
es euch einfach mal an, so schwer ist es nicht:
kommen auch in der Integralrechnung
vor. Um diese Art der DGL lösen zu können, solltet ihr deshalb mit der
Integralrechnung vertraut sein. Die Integralrechnung ist die Umkehrrechnung der
Differenzialrechnung. Mit diesem Wissen können wir die Gleichung lösen. Schaut
es euch einfach mal an, so schwer ist es nicht:
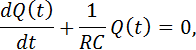
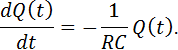
Nun sortieren wir nach Variablen. Auf die Seite von ![]() müssen alle
müssen alle![]() ’s stehen und auf der Seite von
’s stehen und auf der Seite von ![]() müssen alle
müssen alle ![]() ’s stehen. Euer Ziel ist am Ende den
Ladungsverlauf
’s stehen. Euer Ziel ist am Ende den
Ladungsverlauf ![]() zu berechnen, deshalb ist es einfacher, wenn ihr alle
Konstanten auf die Seite von
zu berechnen, deshalb ist es einfacher, wenn ihr alle
Konstanten auf die Seite von ![]() und umstellt:
und umstellt:

Um nun das ![]() und
und ![]() loszuwerden, müssen wir als nächstes integrieren. Konstanten
können wir dabei vor das Integral schreiben:
loszuwerden, müssen wir als nächstes integrieren. Konstanten
können wir dabei vor das Integral schreiben:
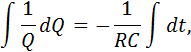
![]()
Beim Integrieren werden immer die Grenzen eingetragen. Diese
werden bei Differenzialgleichungen meisten durch Anfangs- bzw. Randbedingungen
vorgegeben, die in der Aufgabenstellung stehen. Da wir hier keine Werte haben,
verwenden wir die zwei Konstanten ![]() und
und ![]() als untere und die Variablen
als untere und die Variablen ![]() und
und ![]() als obere Grenzen:
als obere Grenzen:
![]()
![]() ist dabei wieder eine Konstante, die wir jetzt der
Einfachheit wegen
ist dabei wieder eine Konstante, die wir jetzt der
Einfachheit wegen ![]() nennen. Als nächstes möchten wir den Logarithmus
eliminieren, dh. wir verwenden die e-Funktion:
nennen. Als nächstes möchten wir den Logarithmus
eliminieren, dh. wir verwenden die e-Funktion:
![]()
![]()
![]()
Auch hier ist ![]() nur eine Zahl, wodurch wir sie wieder als neue Konstante
definieren können. Um einen sinnvollen Namen zu finden betrachten wir einfach
mal die aktuelle Gleichung. Wenn wir unseren Entladevorgang starten, dann gibt
es einen Zeitpunkt
nur eine Zahl, wodurch wir sie wieder als neue Konstante
definieren können. Um einen sinnvollen Namen zu finden betrachten wir einfach
mal die aktuelle Gleichung. Wenn wir unseren Entladevorgang starten, dann gibt
es einen Zeitpunkt ![]() , an dem unsere Betrachtung startet. Das heißt, unser t kann
nur positiv sein, wodurch der Exponent von e immer negativ sein wird und somit
die gesamte Exponentialfunktion für große
, an dem unsere Betrachtung startet. Das heißt, unser t kann
nur positiv sein, wodurch der Exponent von e immer negativ sein wird und somit
die gesamte Exponentialfunktion für große ![]() gegen 0 strebt. Unsere Konstante
gegen 0 strebt. Unsere Konstante ![]() beschreibt also unseren Startwert bei
beschreibt also unseren Startwert bei ![]() , der durch unsere Potenz immer kleiner wird. Deshalb bietet
sich die Bezeichnung
, der durch unsere Potenz immer kleiner wird. Deshalb bietet
sich die Bezeichnung ![]() an, da sie die Ladung beschreibt, welche zum Zeitpunkt
an, da sie die Ladung beschreibt, welche zum Zeitpunkt ![]() auf dem Kondensator ist. Damit
folgt:
auf dem Kondensator ist. Damit
folgt:
![]()
Setzen wir diesen Verlauf von ![]() in die bekannten Formeln ein, so
erhalten wir auch die Verläufe von
in die bekannten Formeln ein, so
erhalten wir auch die Verläufe von ![]() und
und ![]() :
:
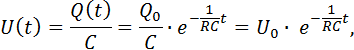
![]()
Bitte wundert euch nicht über das negative Vorzeichen beim Strom. Schließlich fließt der Entladestrom entgegengesetzt zum Ladestrom.
2. Halbwertszeit:
Die Halbwertszeit ist die Zeit t, bei der eine exponentielle
Größe (hier ![]() ), auf die Hälfte gesunken ist. Sie kann folgenderweise
bestimmt werden:
), auf die Hälfte gesunken ist. Sie kann folgenderweise
bestimmt werden:
![]()
![]()
![]()
![]()
Bei der Umformung der Gleichung haben wir angewandt, dass der
natürliche Logarithmus die Umkehrfunktion der E-Funktion ist. Außerdem gilt
beim Logarithmus folgende Umformung: ![]() bzw.
bzw. ![]() .
.
3. Aufladen:
Wie zuvor gilt
![]()
Dabei ist ![]() die Ladespannung, welche nicht zeitabhängig ist. Hier liegt
keine homogene DGL vor, denn auf der linken Seite der Gleichung steht noch eine
Konstante. Was wir aber machen können, ist die gesamte Gleichung zu differenzieren
und danach
die Ladespannung, welche nicht zeitabhängig ist. Hier liegt
keine homogene DGL vor, denn auf der linken Seite der Gleichung steht noch eine
Konstante. Was wir aber machen können, ist die gesamte Gleichung zu differenzieren
und danach ![]() und nicht
und nicht ![]() zu betrachten:
zu betrachten:
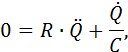
![]()
Nun haben wir durch ![]() eine homogene DGL erhalten, welche wir wie zuvor lösen
können:
eine homogene DGL erhalten, welche wir wie zuvor lösen
können:
![]()
Als nächstes können wir uns nochmals die Grundgleichung zur
Zeit ![]() anschauen:
anschauen:
![]()
Denn die Ladespannung liefert zu diesem Zeitpunkt genau den
Strom ![]() . Also folgt für unsere Gleichung:
. Also folgt für unsere Gleichung:
![]()
![]() beschreibt gerade die Spannung am Kondensator und ist
zeitabhängig. Durch Umstellen der Gleichung können wir
beschreibt gerade die Spannung am Kondensator und ist
zeitabhängig. Durch Umstellen der Gleichung können wir ![]() berechnen:
berechnen:
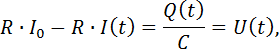
![]()
![]()
![]()